पिंगलको छन्दसूत्रमा गणित

पूर्वीय संंस्कृत साहित्यको रचनामा गणितको व्यापक प्रयोग हुने गरेको पाइन्छ । छन्दशास्त्रका रचयिता ऋषि पिंगलले आफ्नो रचनामा पूरै गणितीय सूत्रहरुको प्रयोग गरेबाट गणित र छन्दको अन्तरसम्बन्ध कति गहिरो रहेछ भन्ने स्वतःसिद्ध हुन्छ ।

बाइनरी प्रणालीमा सम्पूर्ण अंक जगतलाई शून्य र एक गरी दुईवटा चिन्हबाट परिभाषित गरेझैं छन्दशास्त्रमा सम्पूर्ण अक्षरहरुलाई लघु र गुरू गरी उच्चारण भेदका आधारमा दुई भागमा वर्गीकृत गरी सोहीअनुसार सम्पूर्ण छन्दहरुको रचना गर्ने गरिन्छ । छन्दलाई मनन र गायनयोग्य बनाउन लघु र गुरूलाई तीनतीन वटा समूहमा वर्गीकृत गर्दै त्यही वर्ग संख्याको आधारमा छन्दको नामकरण गरिएको हुन्छ । यस्ता तीनतीन वटा समूहलाई पिंगलको छन्दसूत्रमा गण नाम दिइएको छ । सारमा भन्नुपर्दा लघु र गुरूलाई तीन वटा आवृत्तिमा एकबद्ध गरी यी गणहरुको संख्याको आधारमा विभिन्न प्रकारका छन्दहरु रचना गर्ने गरिन्छ । आधुनिक गणितको भाषामा परम्युटेशन र कम्बिनेशनकोे सुन्दर प्रयोग पिंगलको छन्दसूत्रमा गरिएको छ ।

लघु र गुरू एक्लै-एक्लै रहँदा दुईवटा समूह सिर्जना हुन्छ । लघु र गुरू दुईदुई पटक सँगसँगै दोहोरिँदा चार वटा समूह सिर्जना हुन्छन् । लघु र गुरूलाई तीनवटा आवृत्तिमा एकबद्ध गर्दा जम्मा ८ वटा गणसमूहको सिर्जना हुन्छ । लघु र गुरू दुईवटा स्वरलाई तीन अक्षरका दरले कम्बिनेशन गर्दा २३ को सूत्रको प्रयोग गरी ८ वटा गणहरु हुने निर्क्योल पिंगलको छन्दसूत्रमा गरिएको छ ।

यसलाई पिंगलको छन्दसूत्रमा यसरी सूत्रबद्ध गरिएको छ । जहाँ लघुलाई ‘l’ र गुरूलाई ‘S’ चिन्हबाट संकेत गरिएको छ ।

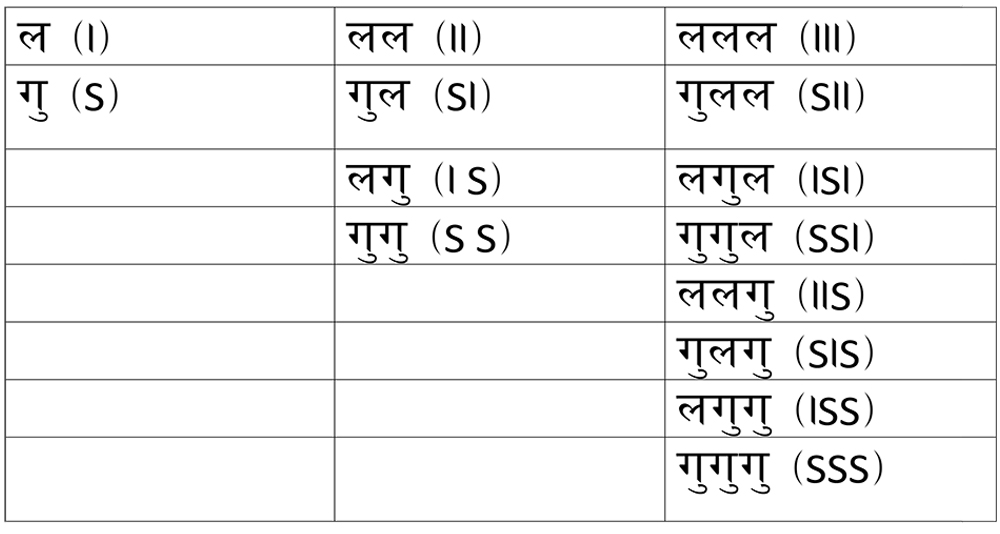
उपरोक्त तालिकालाई निम्नानुसार पिंगलको छन्दसूत्रमा बीज गणितीय सूत्रबाट पनि सिद्ध गरिएको छ ।
(l+S)=l+S
(l+S)²= l²+2lS+S²

यस्तै (l+S)³ को विस्तृत रुपमा रहेको सूत्रको विस्तार यसप्रकार रहेको छः
(l+S)³= l³+3l²S+3S²l+S³
= l l l + l l S +l S l + Sll + S Sl + S lS + lS S + S SS

यसरी (l+S)³ को विस्तार गरी पिंगलको छन्दसूत्रमा गणहरुको सिर्जना गरिएको छ ।

उपरोक्त सूत्रहरुलाई सूत्रबद्ध गर्न पिंगलको छन्दसूत्रमा प्रस्तार मेरुको प्रयोग गरिएको छ ।

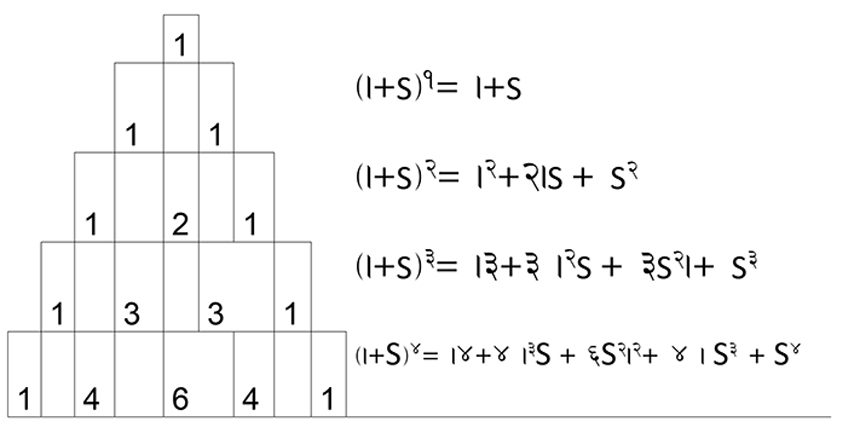
आधुनिक गणितमा पास्कल्स ट्राइएंगल भनी प्रचलित त्रिभुज पिंगलको प्रस्तारको निरन्तरता नै हो (विकिपेडिया) ।

पिंगलको छन्दसूत्रको अर्को सुन्दरतम पक्ष भनेको बाइनोमियल विस्तारको कोफिसियण्टको निर्क्योल पनि हो । जसलाई निम्नानुसार प्रस्ट गर्न सकिन्छ ।

उपरोक्तबमोजिम गणहरुको संख्या र वर्ग निश्चित गरिसकेपछि यसलाई सूत्रबद्ध गर्न प्रत्येक गणको नामकरण गरिएको छ । जसलाई छन्दसूत्रमा यमाताराजभानसलगा उल्लेख गरिएको छ । यो सूत्रबाट गणहरुको सिर्जना गर्दा सुरुमा तीनवटा अक्षरहरुको एउटा गण बनाउने र तत्पश्चात एउटा अक्षर छोड्दै पछिल्ला दुई अक्षरहरु समेट्दै गणहरु नामकरण गरिन्छ । जो यसप्रकार रहेका छन्ः

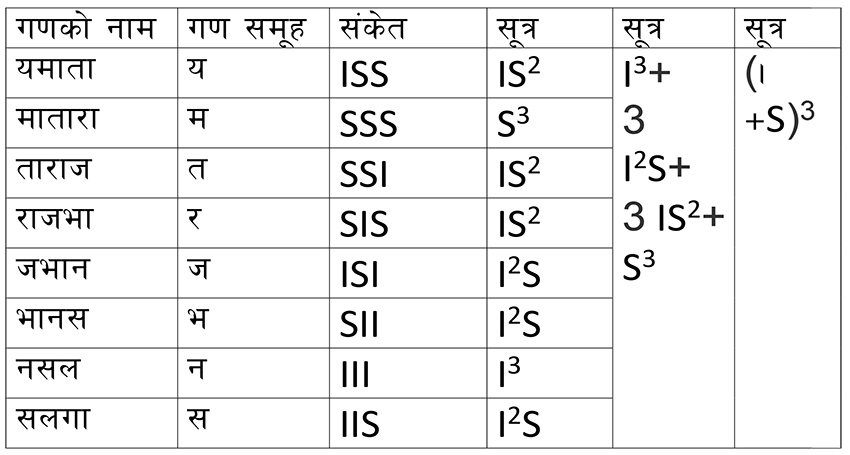
यसरी गणहरुको सिर्जना गरिएको पिंगलको छन्दसूत्रको गण रचनामा प्रयोग भएको श्रेणी आवद्धताको सिद्धान्तलाई आधार मानी पाश्चात्य गणितज्ञ डे ब्रुइजिनले आफ्नै प्रकारको आवद्ध श्रेणीको रचना गरेका छन् । जसलाई डे ब्रुइजिन सिक्वेन्स भनिन्छ (विकिपेडिया) । डे ब्रुइजिन सिक्वेन्सको आधारमा नै स्नायुविज्ञान र मनोविज्ञानमा गरिँदै आएको छ । जहाँ स्टीमुलस अर्डरको प्रभावको जाँच गर्न फङ्सनल म्याग्नेटिक रिजोनेन्स इमेजिङमा यसको उपयोग गरिन्छ । भनाइको तात्पर्य जसरी छन्दमा पछिल्लो एक छोड्दै अघिल्लो दुईवटा अक्षर लिएर गण रचना गरिन्छ र एउटा लयबद्ध श्रेणी तयार हुन्छ । त्यसरी नै स्टीमुलसमा पनि पछिल्लो एउटा स्टीमुलस छोड्दै अघिल्लो दुईवटा स्टीमुलस अंगीकार गर्दै जाँदा निरन्तरतायुक्त जुन आवृत्ति रेखा खिचिन्छ । त्यही नै गण रचनाको सिद्धान्तमा आधारित छ ।

वर्तमान श्रेणी शास्त्रको महत्वपूर्ण अंग मानिएको फिबनाची श्रेणाको उद्गम पनि पिंगलको छन्दसूत्र नै रही आएको छ । मिश्रौ च भन्ने सूत्रका आधारमा ०, १, १, २, ३, ५, ८, १३, २१, ३४, ५५, ८९, १४४, …, …. को श्रेणी बन्न जाने सूत्रको पहिलो प्रयोग पिंगलको छन्दसूत्रमा गरिएको छ ।

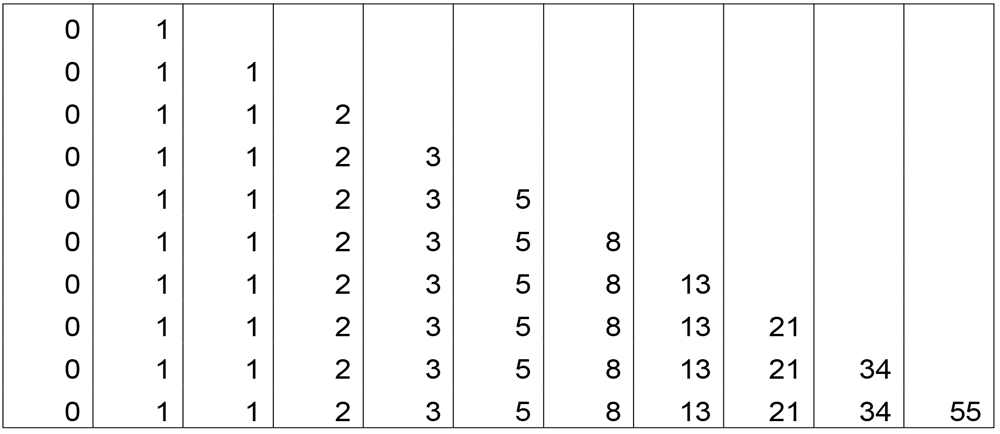
उपरोक्त तालिकाअनुसार हरेक पछाडिका दुईवटा अंकहरु जोड्दै नयाँ श्रेणीको संख्या राख्ने विधिको उत्कृष्ट नमुना पिंगलको छन्दसूत्रमा रहेको छ ।

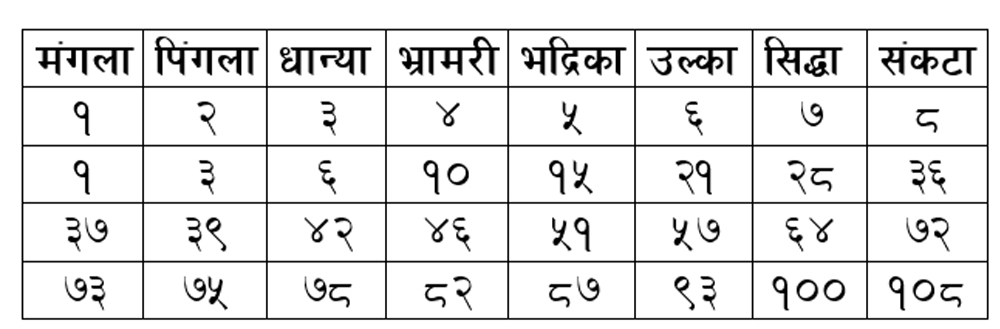
ज्योतिष विज्ञानमा दशाको वर्ष गणना पनि यही विधिबाट हुने गर्दछ । इष्ट दशा निर्धारण गरिसकेपछि पछिल्ला वर्षहरु अघिल्लो वर्षसँग पछिल्ला वर्षहरुको योग निकाल्दै ३६, ७२ र १०८ वर्षसम्मको दशा निकाल्ने गरिन्छ । जहाँ मंगला, पिंगला, धान्या, भ्रामरी, भद्रिका, उल्का, सिद्धा र संकटालाई १ देखि ८ सम्मको अंक दिइन्छ । जसको संरचना यसप्रकार रहेको हुन्छः

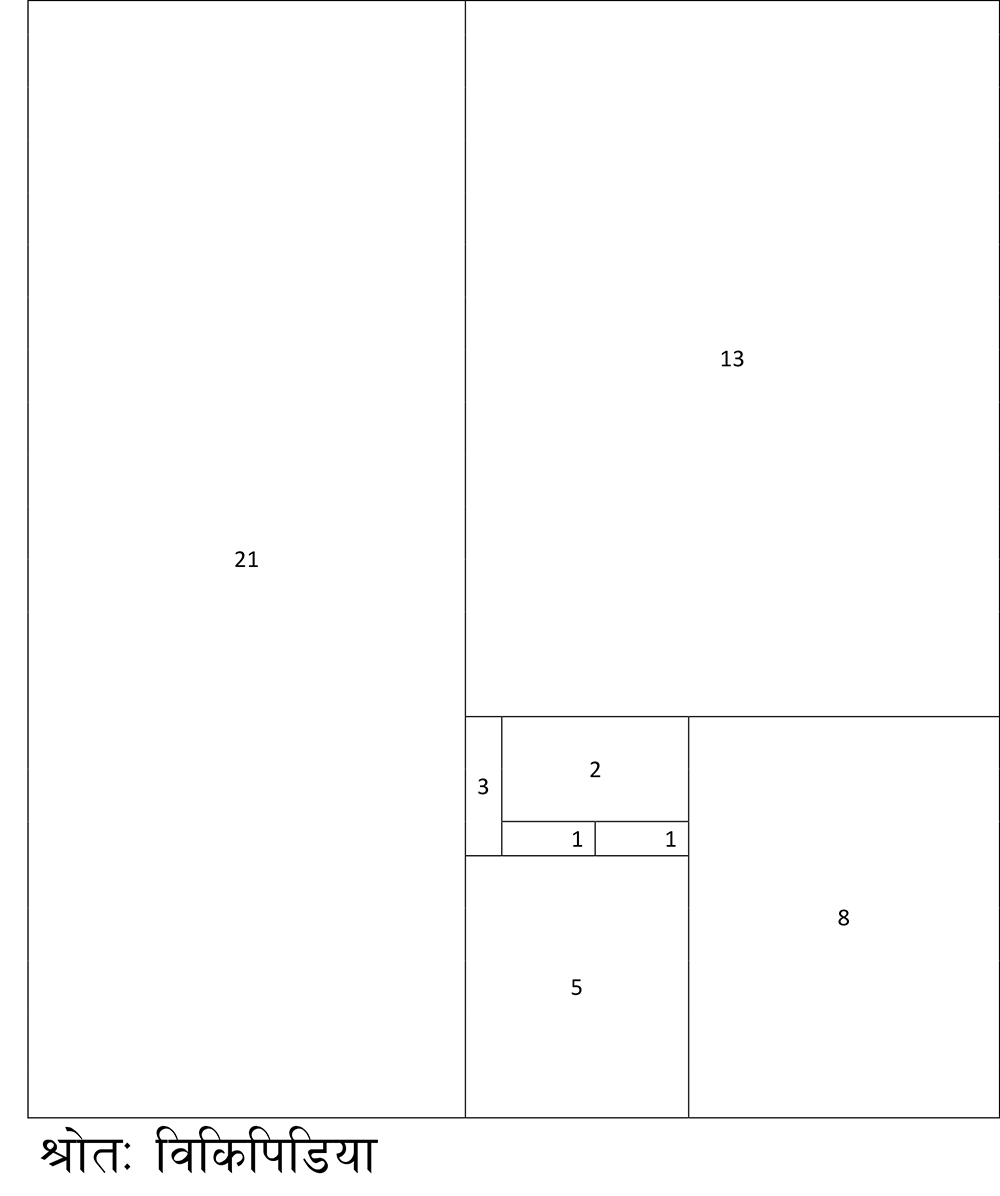
पिंगलको मिश्रौ च सूत्रलाई ग्राफमा प्रयोग गरी रेखाहरुको रचना गर्दा यसको आकार सृष्टियुक्त ब्रह्माण्डको आकारसँग मिल्न जान्छ ।

यसरी प्राचीन समयमा पूर्वीय शास्त्रहरुमा रचनामा गणितको प्रयोगमात्र भएको छैन । यी रचनाहरु तयार गर्दा गणितका सूत्रहरु पनि प्रतिपादित भएका छन् । यी सूत्रमा आधारित रही वर्तमान आधुनिक समाजले थुप्रै वैज्ञानिक आविष्कारहरु गर्न सफल भइरहेको छ ।